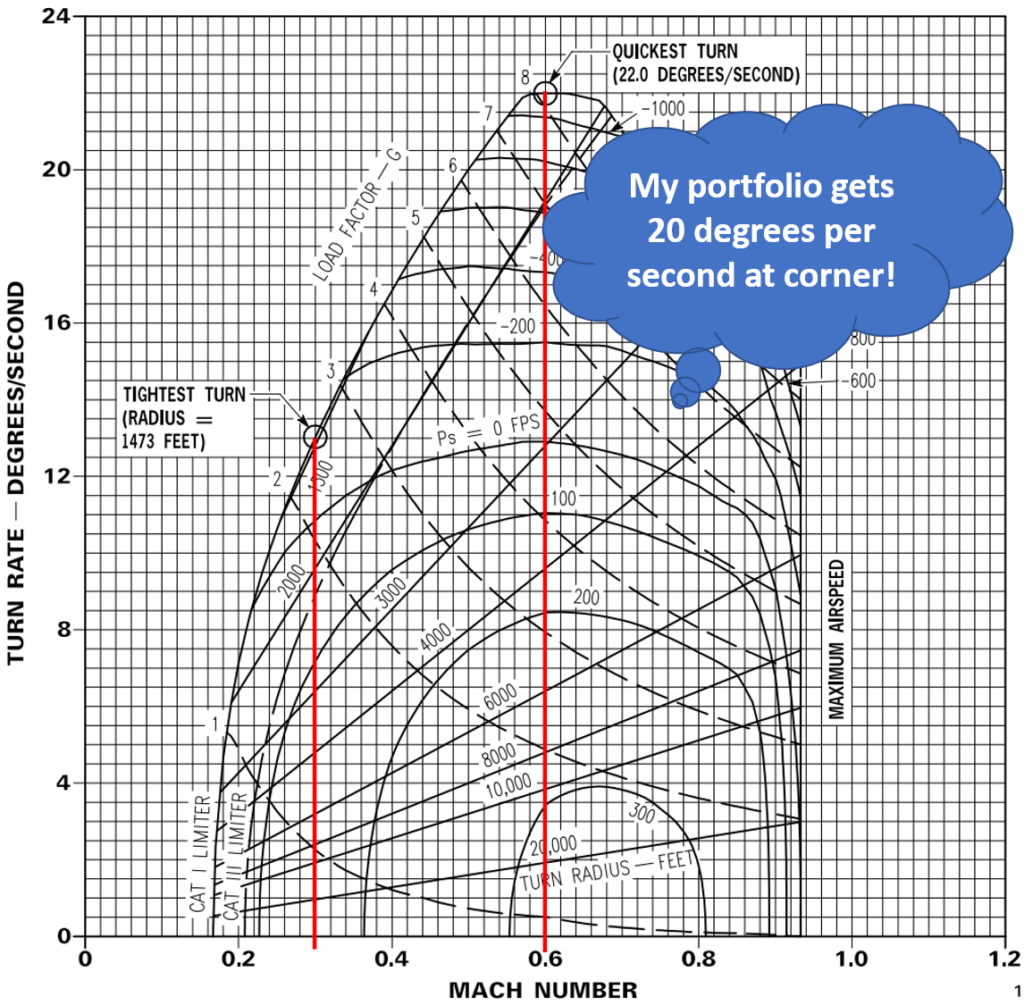
 Rate vs. Radius for Your Portfolio
Rate vs. Radius for Your Portfolio
Nose position versus energy is one of the very first tenets of BFM that we all learn. Expend energy to put the pipper on the target, or preserve energy to enable future maneuvers. Either way, dogfights are a series of tradeoffs of current and future capability. Risk and return decisions in an investment portfolio are similar. Should you take more risk now for the chance to earn more return now? Is it better to preserve risk (energy) for a future use such as purchase of an asset at a temporarily depressed price (or an over-the-top maneuver with the bandit is out of energy)? Hopefully the metaphor isn’t too mixed for you, but let’s take a look at some risk return considerations for a portfolio.
Risk
There are many types of risk and here are some example:
- Business risk: the company may fail or fail to perform
- Legislative risk: Congress may pass a law that harms your investment strategy
- Inflation risk: inflation erodes your returns
- Currency risk: you invest in Iraqi Dinar and the government defaults
- Interest rate risk: rates go the wrong direct for your needs/strategy
- Reinvestment rate risk: you can’t get as high of a return on your bond yields as you needed
- Tax risk: tax rates go up and your Traditional/Roth decision was wrong
- Investment manager risk: your active fund manager fails to perform as needed
- Liquidity risk: the crowd-funded real estate investment holds on to your cash 3 extra years
- Country risk: Venezuela nationalizes the oil industry and you held too much Exxon
- Market risk: Volatility swings the wrong way for your current needs
- Sequence of returns risk: The first three years of your retirement are 2007-2009 and now you have to go back to work…
This list is nowhere near inclusive, but investors should be aware of the types of risk they face in order to mitigate them. Most of the risks on this list are successfully managed through various forms of diversification. Even sequence of returns risk can be mitigated with adequate cash if the portfolio and income needs permit. For this article however, we’ll focus mostly on Market Risk or volatility—the constantly changing prices and returns of assets.
As I’ve discussed before, one of the Five Pillars of Investing is investment allocation—diversifying into different asset classes. We know we should probably buy a mix of stocks, bonds, and real estate, but what is the right mix? Clearly, the answer isn’t in a short blog article by a washed-up fighter pilot turned CFP®, but here are some thoughts that can help as you work through the compendium of knowledge in books, podcasts, websites, etc.
Sharpe Ratio
One of the most useful tools in evaluating investments, especially mutual funds and ETFs, is the Sharpe Ratio. Let’s imagine that you could invest in a truly risk-free investment, like the 90-day Treasury Bill. There is virtually no chance that your investment in this risk-free vehicle won’t return what it’s supposed to return (your principal and some stated amount of interest). The risk-free investment probably doesn’t provide much return, but it doesn’t provide any risk. Let’s imagine that you also invest in (hypothetical) ABC mutual fund, a compilation of 580 of the largest American company stocks. ABC’s value and returns (dividends) fluctuate with the value and dividends of the underlying companies. We know that stock returns are generally higher than Treasury Bill (and other fixed-income instruments) returns, but we also know that the risk or volatility of prices and returns for stocks is higher too. The problem we face in asset allocation is “How to quantify risk and return?” The answer? Use a method to determine just how many units of return your investment provides for each unit of risk it requires. Wait, huh?
Let’s define return as the expect return from an investment in percentage terms. For example, we expect based on research, that ABC mutual fund will return 10% going forward, and we expect the risk-free investment to return 1%.
Let’s also define the expected risk or volatility of each asset as the standard deviation—the amount that the investment should be expected to go up or down in a year based on historical performance. Suppose that ABC has a standard deviation of 15% and the risk-free asset has a standard deviation of 0% (it’s risk-free, remember?) This data is widely available on brokerage websites for assets, so it’s not like you need to dust off the ol’ stats text book to gonk the data.
Sharpe Ratio is calculated by subtracting the risk-free return from the expected return of ABC, then dividing by the standard deviation of ABC.
(10% – 1%) ÷ 15% = .6
Sharpe Ratio by itself is almost meaningless. To say that a given asset’s Sharpe Ratio is .6 is as useful as “Bears beets Battlestar Galactica.” But mathematically, we can see that Sharpe Ratio shows us that an investment in ABC should provide .6 units of return for each unit of risk. It’s a risk-adjusted return of an investment.
Now, let’s say we could alternatively invest in XYZ mutual fund with an expected return of 8% and a standard deviation of 6%. Its Sharpe Ratio would be:
(8% – 1%) ÷ 6% = 1.17
XYZ doesn’t deliver as much return, but it delivers much more return per unit of risk. Thus, for any two investments, a comparison of Sharpe Ratios can help normalize two different expected returns against two different expected risks. Generally, for similar investments, one will prefer the investment with the higher Sharpe Ratio. For different investments such as a stock fund and bond fund, Sharpe Ratio isn’t as useful.
Building Blocks
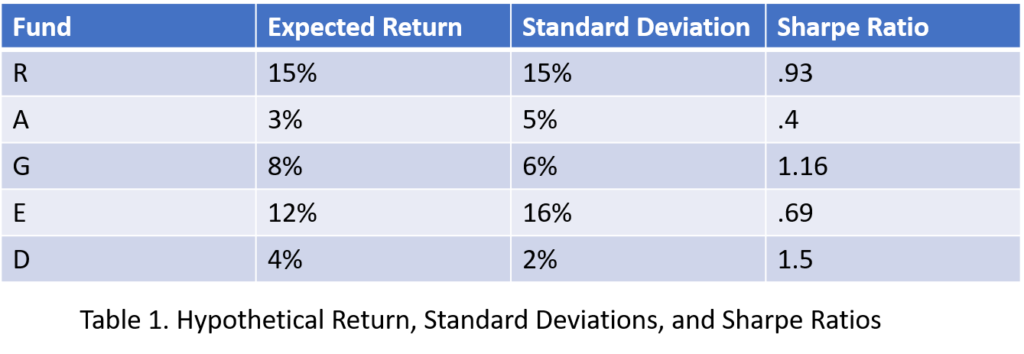
What if you had an employer-provided, qualified account that only offered 5 funds, or various time-balanced combinations of those funds, and you could either invest in those funds or a risk-free asset that returns 1%? Additionally, what if you needed to achieve a 7% nominal (pre-inflation) rate of return on your portfolio in order to achieve your retirement funding goal? And what if you found that the expected returns and standard deviations of the funds looked like Table 1? How could you construct a portfolio that would be expected to achieve at least 7% nominal return with the lowest risk?
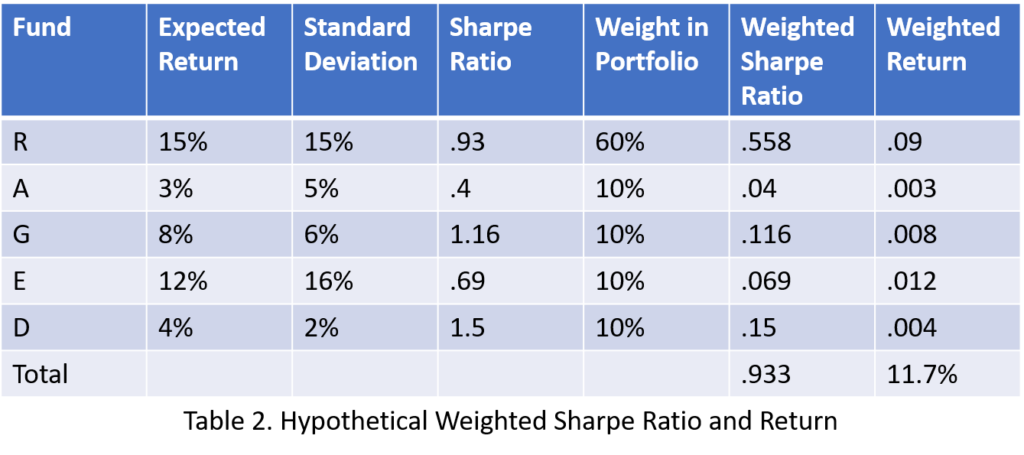
The methodology would require determining what mix of the funds (e.g. 20% of each) would provide the highest return and Sharpe Ratio. Tables 2 and 3 explore different asset allocations or weights with this hypothetical 5-fund portfolio. Table 2 weighs the “R-Fund” most heavily at 60% of the portfolio, so its return and Sharpe Ratio carry the most influence on the weighted return and Sharpe Ratio of the portfolio. As such, the weighted return of the portfolio is 11.7%.
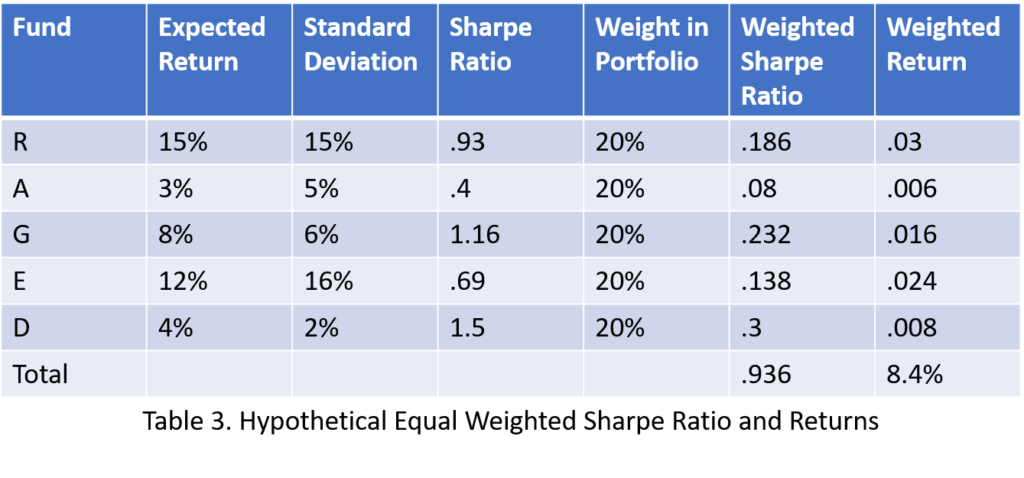
Table 3 evaluates an equal-weighed portfolio, where the investor just chose a flat 20% of each fund for the portfolio. Because the highest-performing “R Fund” receives less weight in this portfolio, the weighted return is much lower at 8.4%
Interestingly, the weighted Sharpe Ratios of the portfolios are nearly identical, which makes selection between the two portfolios easy—an investor would choose the higher-returning portfolio since it has the same risk-adjusted return as the lower performing portfolio. It’s not hard to imagine, given that there are thousands of stocks, bonds, and funds in the market, that other portfolios will deliver significantly different results. If your analysis constructed two portfolios with equal weighted returns, but meaningfully different Sharpe Ratios, then the portfolio with the higher Shape Ratio should deliver superior risk-adjusted returns.
Summary
Choosing how to allocate risk and return when selecting investments is not unlike determining how to fight a given adversary. Turn rate and radius both factor into how to max-perform the jet in order to kill and survive. Risk and return need to be built into investment selection choices too. By introducing Sharpe Ratio into your thought process, it’s possible to determine risk-adjusted returns. Sharpe Ratio can help you understand whether you’ll likely be compensated for any extra risk you choose to take when comparing dissimilar investments. Fight’s On!
Winged Wealth Management and Financial Planning LLC (WWMFP) is a registered investment advisor offering advisory services in the State of Florida and in other jurisdictions where exempted. Registration does not imply a certain level of skill or training.
This communication is for informational purposes only and is not intended as tax, accounting or legal advice, as an offer or solicitation of an offer to buy or sell, or as an endorsement of any company, security, fund, or other securities or non-securities offering. This communication should not be relied upon as the sole factor in an investment making decision.
Past performance is no indication of future results. Investment in securities involves significant risk and has the potential for partial or complete loss of funds invested. It should not be assumed that any recommendations made will be profitable or equal the performance noted in this publication.
The information herein is provided “AS IS” and without warranties of any kind either express or implied. To the fullest extent permissible pursuant to applicable laws, Winged Wealth Management and Financial Planning (referred to as “WWMFP”) disclaims all warranties, express or implied, including, but not limited to, implied warranties of merchantability, non-infringement, and suitability for a particular purpose.
All opinions and estimates constitute WWMFP’s judgement as of the date of this communication and are subject to change without notice. WWMFP does not warrant that the information will be free from error. The information should not be relied upon for purposes of transacting securities or other investments. Your use of the information is at your sole risk. Under no circumstances shall WWMFP be liable for any direct, indirect, special or consequential damages that result from the use of, or the inability to use, the information provided herein, even if WWMFP or a WWMFP authorized representative has been advised of the possibility of such damages. Information contained herein should not be considered a solicitation to buy, an offer to sell, or a recommendation of any security in any jurisdiction where such offer, solicitation, or recommendation would be unlawful or unauthorized.
